Gaussian Processes

Author(s): Ryan-Rhys Griffiths is currently a postdoctoral research scientist at Meta Research where he works on Bayesian optimization and Gaussian processes as part of the Adaptive Experimentation (BoTorch!) team. Previously he was a research scientist at Huawei Noah’s Ark Lab and completed his PhD in Machine Learning and Physics at the University of Cambridge. Ryan is broadly interested in molecular machine learning, astrophysics, materials science and many more!

Introduction

Gaussian processes (GPs) [1] are a central model in probabilistic machine learning with particularly favourable properties for uncertainty quantification and Bayesian optimisation [2, 3, 4]. To date, however there has been little investigation into GPs applied to conventional representations of molecules such as fingerprints [5], SMILES strings [6, 7] and graphs. In this blogpost, I showcase some of the use-cases for GPs in chemistry using GAUCHE [8, 9], an open-source library implementing GPs kernels that allow GPs to operate on molecular representations. Such use-cases include the representation of model uncertainty in virtual screening where one wishes to prioritise molecules or materials for laboratory synthesis based on machine learning property prediction. In this setting, using model uncertainty to assess how likely the model is to be wrong about its prediction can expedite discovery efforts.

Figure 1: Gaussian process regression over molecular space.

Gaussian Processes

A GPs is a stochastic process which, in a machine learning context, is used to represent a distribution over functions that may explain a set of observed data. The focus of this section is on the properties of GPs that make them useful in the context of chemistry. For an exhaustive technical introduction to GPs the reader is referred to [1] and to a [10] for a slightly more accessible introduction. I also recommend the following distill article as an excellent aid for understanding the concepts behind GPs which can often be challenging on first presentation due to the need to think in different spaces (data space, the space on which the multivariate Gaussian distribution is defined, heatmaps of covariance matrices etc.). https://distill.pub/2019/visual-exploration-gaussian-processes/

How do Gaussian Processes Work Roughly?

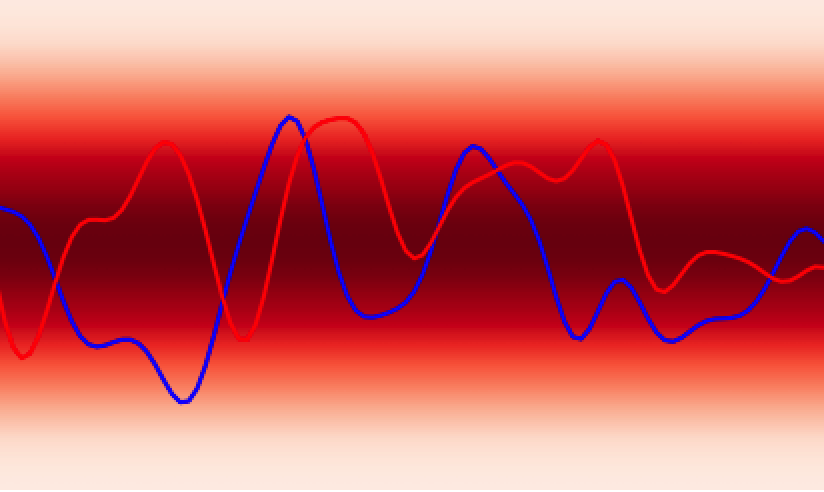
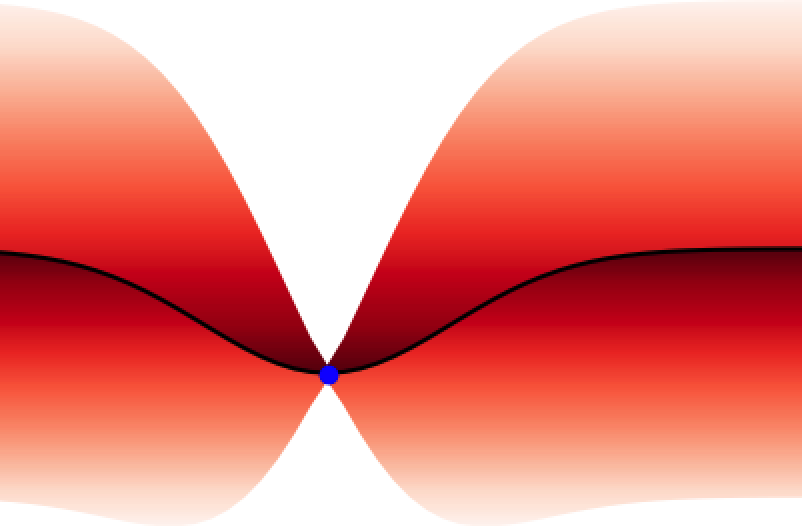
In analogy to a neural network, the GPs prior encodes the hypothesis space (set of functions that could explain the data) of the GPs in much the same way as the choice of architecture (number of layers, activation functions) defines the hypothesis space of a neural network. While these hypothesis spaces are often sufficiently broad to encompass a wide range of functions, it can sometimes be difficult to find (learn) these functions given a dataset; this is the machine learning model optimisation problem and the choice of initial GPs prior or network architecture can make this optimisation problem easier or harder. In continuous spaces, an object called the GPs kernel plays a central role in determining the nature of the GPs prior hypothesis space. As an example, in , the squared exponential kernel (SQE) encodes a hypothesis space that prioritises smoother functions relative to the Matérn kernel.

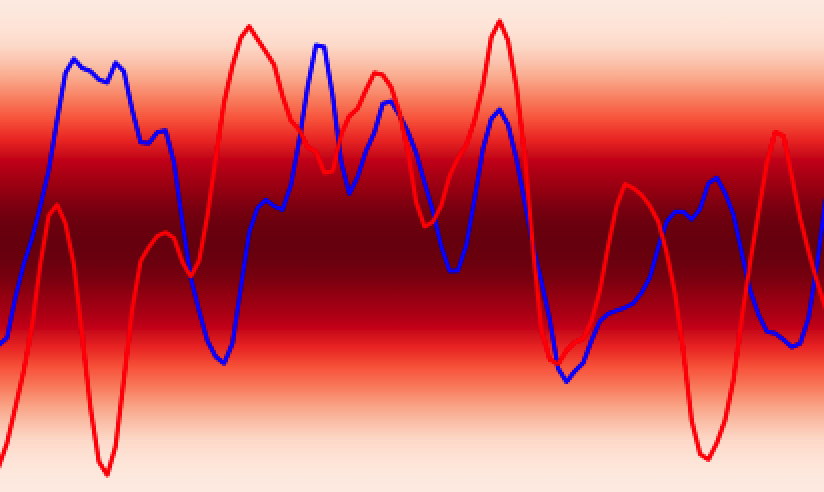
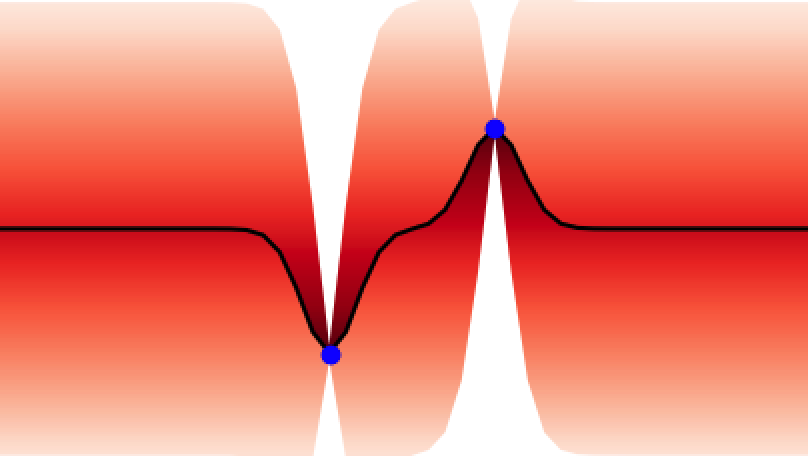
Figure 2: A comparison of the SQE and Matérn 5/2 kernels. Shading indicates a GPs prior distribution over functions (defined by the choice of kernel) and the solid red and blue lines are individual draws from the distribution over functions. The SQE kernel represents a hypothesis space containing smoother functions relative to the Matérn 5/2 kernel. Reprinted with permission from [11].

Additionally, GPs kernels possess hyperparameters that control the behaviour of the functions and may be learned from the data. As an example, in Figure 3 the lengthscale hyperparameter controls how quickly the functions vary across the input space.

Figure 3: (a) SQE small lengthscale, (b) SQE large lengthscale.

Why Should We Fit a Gaussian Process Instead of a Neural Network?

One might reasonably ask what advantagesGPs can afford over neural networks? While deep learning methods represent the state-of-the-art for large datasets, for small datasets, deep learning may often not be the methodology of choice. Indeed some notable deep learning experts have voiced a preference for GPs in the small data regime[12]. Furthermore, GPs possess advantages relative to neural networks in representing uncertainty and in their ease of training; GPs admit exact Bayesian inference and few of their parameters need to be determined by hand. In the words of Sir David MacKay [13],

“Gaussian processes are useful tools for automated tasks where fine tuning for each problem is not possible. We do not appear to sacrifice any performance for this simplicity.”

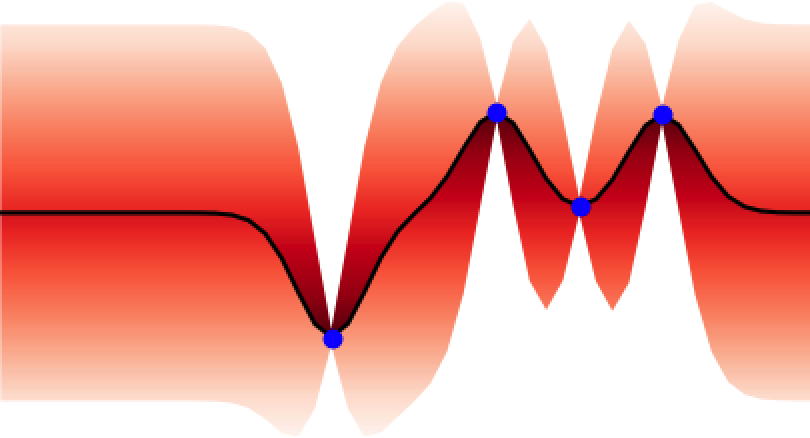
These properties make GPs ideal for uncertainty quantification and as surrogate models for Bayesian optimisation BO, an algorithm that is showing promise for scientific discovery in the search for novel molecules[14], materials, and optimal chemical reaction conditions [15,16]. An illustration of the GP’s ability to represent uncertainty is given in Figure 4 where one can observe how the GP updates its predictive uncertainty based on the data it has observed. This property makes GPs useful for a wide range of chemical applications.

Figure 4: An illustration of the GP posterior update on fitting 1, 2 and 4 data points (Blue). The posterior distribution encodes the distribution over possible functions that may explain the data. Reprinted with permission from [11].

Adapting Gaussian Processes for Chemistry

While the above examples consider GPs defined on continuous input spaces, it is possible to defineGPs on discrete molecular representations as well via the choice of GP kernel. Two recent libraries, FlowMO (Tensorflow) [8], and GAUCHE (PyTorch) [9] open-source several molecular GP kernels that operate on a range of molecular and chemical reaction representations.

Application

In many virtual screening applications one wishes to have not only a machine learning prediction for unseen regions of the search space but also to know how accurate such a prediction is likely to be. Intuitively one would expect models to be more confident when making predictions around observed data points than when making predictions far away from the training set. In this section we take a look at what GPs can offer in terms of “knowing what they don’t know” when making predictions.

Virtual Screening with Model Uncertainty

It is well known that machine learning models can be employed as molecular property predictors for virtual screening. In addition to providing a predicted property value, however, models can also provide an uncertainty estimate, in other words a measure of the prediction confidence. GPs are typically some of the best-calibrated probabilistic models due to the facility to perform exact Bayesian inference. In order to empirically assess the quality of molecular gp uncertainty estimates, we use a diagnostic tool known as a confidence-error curve [17] (also featured in the Jupyter notebook demo). The confidence-error curve for the SMILES string kernel is given in Figure 5. The TLDR is that the model achieves smaller prediction error on test molecules for which it has higher confidence.

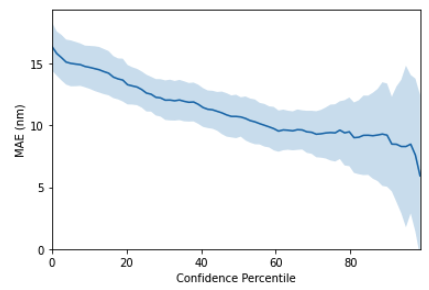
Figure 5: GP confidence error curve. The x-axis, Confidence Percentile, ranks each test datapoint prediction according to the GP predictive variance. For example, molecules that reside above the 80th confidence percentile will correspond to the 20\% of test set molecules with the lowest GP predictive uncertainty. The prediction error at each confidence percentile is then measured over 20 random train/test splits (the standard error over the random splits is plotted in the figure above) to gauge if the model’s confidence is correlated with the prediction error. This figure shows that the SMILES GP’s uncertainty estimates are positively correlated with the prediction error. As such, it is possible that model uncertainty could be used as a component in the decision-making process for prioritising molecules for laboratory synthesis. A natural extension to the idea of using model uncertainty to prioritise the immediate next choice of molecule for laboratory synthesis is to automate a sequence of choices, feeding each queried molecule back into the GP model to provide a better model for the next step in an iterative fashion. This is the idea behind Bayesian optimisation.

A natural extension to the idea of using model uncertainty to prioritise the immediate next choice of molecule for laboratory synthesis is to automate a sequence of choices, feeding each queried molecule back into the GP model to provide a better model for the next step in an iterative fashion. This is the idea behind Bayesian optimisation.

Bayesian Optimisation

The uncertainty estimates produced by a GP can be leveraged directly to accelerate scientific discovery via a scheme called Bayesian optimisation [3]. Informally, Bayesian optimisation (BO) aims to quickly identify promising molecules or materials by using model uncertainty estimates to explore a space of candidates to be prioritised for laboratory synthesis. Formally, Bayesian optimisation may be described as a solution method for a black-box global optimisation problem

\[\mathbf{x}^{\star} = \arg\max_{\mathbf{x} \in \mathcal{X}} f(\mathbf{x})\]

where \(f:\mathcal{X} \rightarrow\mathbb{R}\) is a function over an input space \(\mathcal{X}\). \(\mathcal{X}\) is discrete for molecular representations such as graphs and strings. Equation above is a black-box optimisation problem when the following properties hold:

Black-Box Objective: The analytic form of \(f\) and its gradients are unavailable. We may, however, evaluate \(f\) pointwise anywhere in the input space \(\mathcal{X}\).
Expensive Evaluations: Evaluating \(f(\mathbf{x})\) at a given molecule \(\mathbf{x}\) takes a long time or incurs a large financial penalty.
Noise: Evaluation of a molecule \(\mathbf{x}\) is a noisy process.

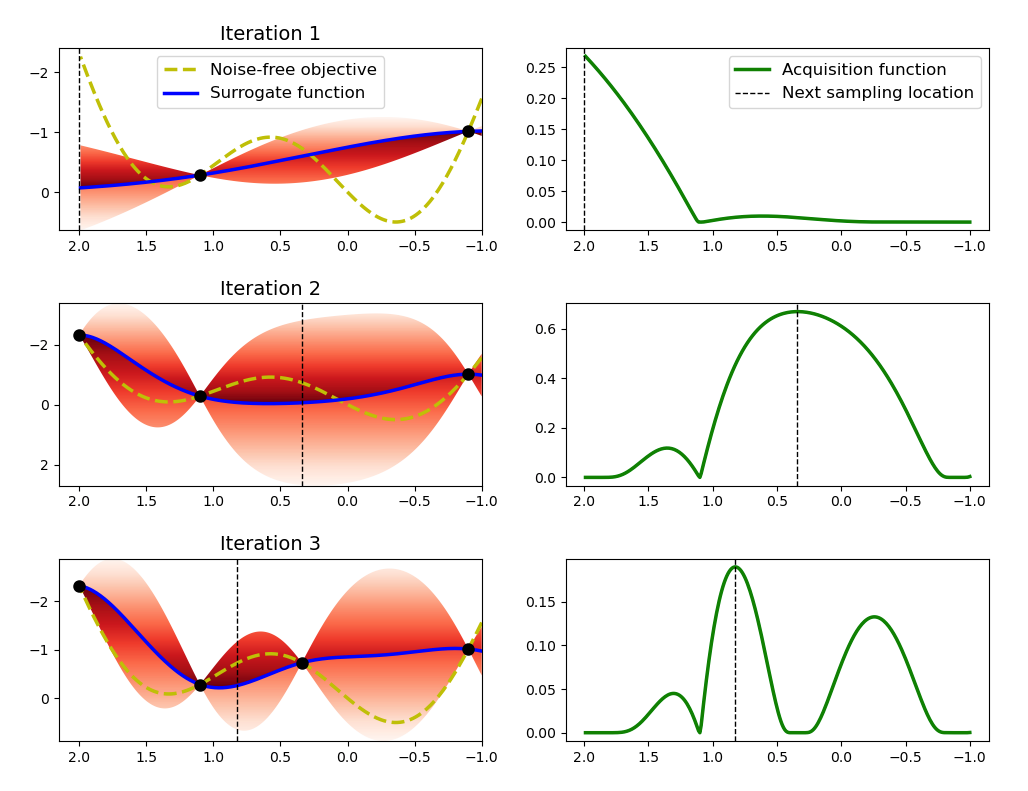
Figure 6: An illustration of the Bayesian optimisation algorithm. Reprinted with permission from [11].

BO is a solution method for such black-box optimisation problems comprised of a probabilistic surrogate model and an acquisition function. The surrogate model is fit to a dataset of pointwise observations from the unknown black-box function and the acquisition function suggests new inputs to query based on the model’s predictions and uncertainties (exploitation vs. exploration). The BO algorithm is illustrated graphically in Figure 6.

BO has been successfully employed in a number of scientific domains including molecule generation [14], drug discovery [18], as well as chemical reaction condition optimisation [15].

Jupyter Notebook Demos

The following Jupyter notebook demos go into greater detail on the mechanics of GP regression, uncertainty quantification and Bayesian optimisation over molecular spaces.

Reference

[1] Christopher K Williams and Carl Edward Rasmussen. Gaussian processes for machine learning. MIT press Cambridge, MA, 2006.

[2] Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P Adams, and Nando De Freitas. Taking the human out of the loop: A review of Bayesian optimization. Proceedings of the IEEE, 104(1):148–175, 2015.

[3] Roman Garnett. Bayesian Optimization. Cambridge University Press, 2022. in preparation.

[4] Antoine Grosnit, Alexander Imani Cowen-Rivers, Rasul Tutunov, Ryan-Rhys Griffiths, Jun Wang, and Haitham Bou-Ammar. Are we forgetting about compositional optimisers in Bayesian optimisation? J. Mach. Learn. Res., 22:160–1, 2021.

[5] David Rogers and Mathew Hahn. Extended-connectivity fingerprints. Journal of Chemical Information and Modeling, 2010.

[6] Eric Anderson, Gilman D Veith, and David Weininger. SMILES, a line notation and computerized interpreter for chemical structures. Environmental Research Laboratory, 1987.

[7] David Weininger. SMILES, a chemical language and information system. 1. introduction to methodology and encoding rules. Journal of Chemical Information and Computer Sciences, 1988.

[8] Henry B. Moss and Ryan-Rhys Griffiths. Gaussian Process Molecule Property Prediction with FlowMO. arXiv e-prints, page arXiv:2010.01118, October 2020.

[9] Ryan-Rhys Griffiths, Leo Klarner, Henry Moss, Aditya Ravuri, Sang T. Truong, Bojana Rankovic, Yuanqi Du, Arian Rokkum Jamasb, Julius Schwartz, Austin Tripp, Gregory Kell, Anthony Bourached, Alex Chan, Jacob Moss, Chengzhi Guo, Alpha Lee, Philippe Schwaller, and Jian Tang. GAUCHE: A library for Gaussian processes in chemistry. In ICML 2022 2nd AI for Science Workshop, 2022.

[10] David Duvenaud. Automatic Model Construction with Gaussian Processes. PhD thesis, Computational and Biological Learning Laboratory, University of Cambridge, 2014.

[11] Ryan-Rhys Griffiths. Applications of Gaussian processes at Extreme Lengthscales from Molecules to Black Holes. PhD thesis, University of Cambridge, 2022.

[12] Yoshua Bengio. What are some Advantages of Using Gaussian Process Models vs Neural Networks?, 2011. https://www.quora.com/What-are-some-advantages-of-using-Gaussian-Process-Models-vs-Neural-Networks.

[13] David JC MacKay, David JC Mac Kay, et al. Information theory, inference and learning algorithms. Cambridge University Press, 2003.

[14] Ryan-Rhys Griffiths and Jos ́e Miguel Hern ́andez-Lobato. Constrained Bayesian optimization for automatic chemical design using variational autoencoders. Chemical Science, 11(2):577–586, 2020.

[15] Benjamin J Shields, Jason Stevens, Jun Li, Marvin Parasram, Farhan Damani, Jesus I Martinez Alvarado, Jacob M Janey, Ryan P Adams, and Abigail G Doyle. Bayesian reaction optimization as a tool for chemical synthesis. Nature, 2021.

[16] Bojana Rankovi ́c, Ryan-Rhys Griffiths, Henry B. Moss, and Philippe Schwaller. Bayesian optimisation for additive screening and yield improvements in chemical reactions – beyond one-hot encodings. ChemRxiv, 2022.

[17] Ryan-Rhys Griffiths, Jake L Greenfield, Aditya R Thawani, Arian R Jamasb, Henry B Moss, Anthony Bourached, Penelope Jones, William McCorkindale, Alexander A Aldrick, Matthew J Fuchter, et al. Data-driven discovery of molecular photoswitches with multioutput Gaussian processes. Chemical Science, 13(45):13541–13551, 2022.

[18] Edward O Pyzer-Knapp. Bayesian optimization for accelerated drug discovery. IBM Journal of Research and Development, 62(6):2–1, 2018.

Introduction

Gaussian Processes

How do Gaussian Processes Work Roughly?

Why Should We Fit a Gaussian Process Instead of a Neural Network?

Adapting Gaussian Processes for Chemistry

Application

Virtual Screening with Model Uncertainty

Bayesian Optimisation

Jupyter Notebook Demos

Further Reading

Gaussian Process

Bayesian Optimisation

GPs and BO for Science

Reference