Author(s): Yujia Zheng is a graduate student at Carnegie Mellon University (CMU). His research interests lie primarily in the linear span of causality and machine learning. Currently, he mainly study causal discovery, causal representation learning, structure learning, and deep learning from a causal view. He is the major coordinator of causal-learn, an open-source causal discovery package for Python.

Learning Causations from Observational Data

Identifying the causal relationships that govern various observed phenomena is an essential objective across diverse scientific disciplines, as it helps researchers understand the underlying mechanisms and facilitate principled analysis. For instance, in medical research, scientists strive to uncover the causal links between environmental factors, genetic predispositions, and disease incidence to develop effective treatments and prevention strategies. In this chapter, we briefly introduce computational methods for learning causation from observational data. Because of the relatively high cost of experimental interventions in real-world scenarios, it is desirable to have principled methods to benefit from causality given only observational data. We start with an overview of causal representation learning and causal discovery. Then we describe some instances of applications of causality in science. Finally, we introduce an open-source tool for causal discovery with a quick example of usage. All materials only serve as an informal and incomplete introduction to those who would like to take a glance at the topic, instead of a part of a formal survey.

What is causal representation learning?

Causal representation learning connects the fields of causality and deep learning. Over the past decade, deep learning has become a key technology in AI fields such as computer vision and natural language processing and has also been used to empower various industries such as robotics, autonomous driving, human-computer interaction systems, virtual reality, pharmaceuticals, and smart cities. This method uses neural networks to transform unstructured data such as images and text into representations that can be processed by machines and solve downstream tasks like recognition and understanding. The aim of representation learning is to reduce the dimensionality of high-dimensional raw data to low-dimensional features while preserving information and removing noise.

As scientists, the pursuit of knowledge is at the forefront of our work, and there is a particular fascination with uncovering causal relationships that underlie observed phenomena. With the advent of black-box algorithms that can make accurate predictions without revealing the underlying causal mechanisms, it is becoming increasingly important to discover and understand the causal relationships that drive these predictions. Researchers are interested in developing interpretable learning models that can identify causal relationships between inputs and outputs, enabling greater transparency and control over the decision-making process.

However, the representations learned by scaling up data and model size often only encode, compress, or memorize data. These representations lack higher-order semantic concepts that can be used by machines for logical reasoning and planning and do not have the adaptability and robustness to solve problems in new environments like humans. Consequently, making deep learning capable of conscious reasoning, thinking, and judgment like humans is a crucial challenge for the next generation of AI. On the other hand, causal models provide a systematic and statistical approach to causal reasoning and thinking. Yet, these models typically only handle structured data and cannot process the high-dimensional raw data encountered in real-life scenarios such as images. The fusion of representation learning and causal models, which transforms raw data like images into structured variables usable by causal models, allows AI to reason and think consciously like humans, making it the primary goal of the emerging field of causal representation learning. Solving this problem would enable us to combine causal inference with machine learning and build the next generation of flexible and trustworthy AI.

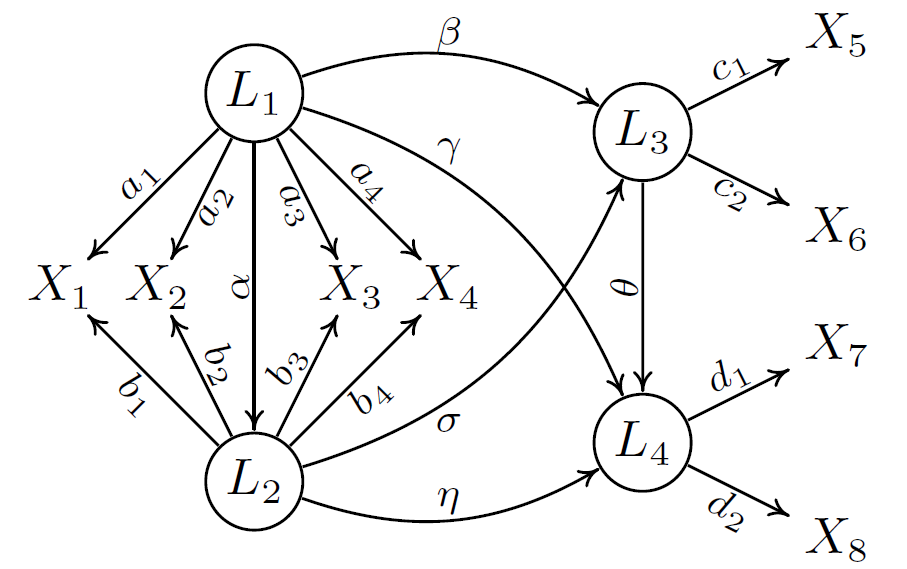
Figure 1: An example of the causal hidden variables (e.g., {L1, L2, L3, L4}).

In causal representation learning, we typically assume that data is generated by causal hidden variables that are related to each other and satisfy certain conditions of a structural causal model (SCM) through nonlinear mapping. If the causal hidden variables and the SCM between them can be learned from the original data, we can estimate the data distribution after intervening on these variables, or infer the counterfactual results of a specified data point, such as generating data that does not exist in the real world by re-combining the causal hidden variables, or answering questions that require explicit reasoning such as “Why” or “What if”. It is worth noting that causal representation learning is closely related to causal discovery. On the one hand, causal representation learning is a special case of the causal discovery problem with many confounders. On the other hand, it is extremely difficult to learn the structural causal model in the entire hidden variable space without domain knowledge. Therefore, the assumptions commonly used in causal discovery, such as Sparsity, Minimal Change Principle, and Independent Causal Mechanism, can often serve as domain knowledge and inductive bias for causal representation learning.

Causal Discovery: Methods and Applications

Discovering and obtaining causal relationships from data has played a crucial role in various disciplines as a fundamental data analysis method in the past few decades. Almost all sciences are about identifying causal relationships and the laws or regularities that govern them. Since the beginning of modern science in the 17th century, there have been two methods for discovering causal relationships: (1) manipulating and changing certain characteristics in a system and observing whether other characteristics change, and (2) observing changes in system characteristics without manipulation. These two methods flourished in the 17th century and were intertwined with each other, as disccused in [1]: “Ivan Johannes Stal-Tolcheli manipulated the angle and shape of a tube containing mercury, but the height of the mercury did not change. Pascal lifted the pressure gauge designed by Tolcheli to a mountain to prove that the height of the mercury did indeed change with altitude. Galileo determined (qualitatively) the orbit of the moon around Europa by observing time series. Kepler derived his three laws of planetary motion from planetary observations. And Newton laid the foundations of modern physics with the law of gravitation, derived from observations of the solar system and a single experiment. Modern molecular biology is an experimental subject, but the foundation of biology, in Darwin’s “Origin of Species”, is based on only one experiment, i.e., the seed drift.”

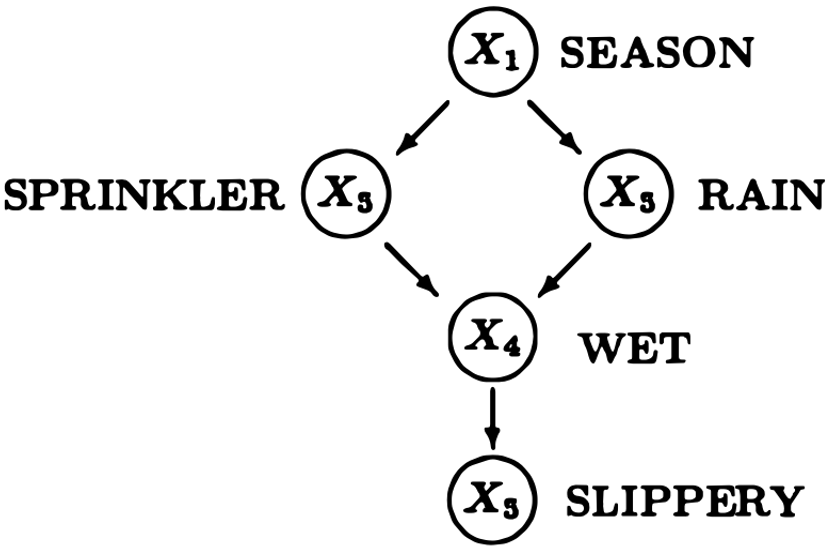
Figure 2: An example of the causal graph.

Classic causal discovery methods are usually used to find causal relationships between observed variables, which can be roughly divided into two categories. At the end of the 1980s and the beginning of the 1990s, it was noticed that, under appropriate assumptions, the latent causal structure could be recovered from the conditional independence relationships between variables in a Markov equivalence class [2]. This has led to constraint-based methods that use conditional independence tests and discrete searches for causal discovery. The resulting equivalence classes may contain multiple directed acyclic graphs (DAGs, or other graph objects that represent causal structures) that share the same conditional independence relationships. The required assumptions include the causal Markov condition and the faithfulness assumption, which establish a correspondence between the d-separation properties in the causal graph and the statistical independence properties in the data. On the contrary, score-based methods [3, 4] are not based on statistical tests, but search for equivalence classes with the highest scores under certain scoring criteria, such as the Bayesian information criterion [5] and the generalized score [6]. Moreover, exact score-based methods [7] can also recover the causal structure in a divide-and-conquer manner.

Another set of methods is based on functional causal model (FCM), which represent the effect as its direct cause and the corresponding independent noise. It has been shown that, with appropriate constraints on the model classes, the direction of the causal effet can be identified. Specifically, when the FCM is estimated in the correct causal direction, the estimated noise term is independent of the hypothesized cause, of which the phenomenon does not hold in the inverse direction. Identifiable causal models include LiNGAM [8], additive noise causal model [9, 10], post-nonlinear causal model [11, 12]. However, it is noteworthy that if the function space of the functional causal model is not constrained, the causal direction cannot be identified [13].

The methods presented above have been extended to more general scenarios. For example, LiNGAM has been extended to causal graphs with loops [14] and in the presence of potential confounders [15]. The specific and shared causal relation modeling [16], which is based on LiNGAM, can provide not only global causal structures but also individualized causal knowledge and clustering based on causal relationships. Also, it is shown that causal models (including causal direction) are possible to identify even in the presence of selection bias [17].

Currently, methods for causal discovery focus on finding causal relationships between observed variables, but in real-world problems, many relevant features may not be observed, and some observed variables may not be latent causal variables. For example, we cannot directly treat image pixels as causal variables. Therefore, as mentioned in the first part, we want to learn the latent causal representation from the measured high-dimensional variables and the causal relationships between them, which is essential in both general artificial intelligence and scientific fields. For example, in AI, we want to automatically extract underlying low-dimensional causal variables or concepts from high-dimensional video sequences, which are crucial for video understanding, thus promoting downstream prediction or decision-making tasks. In neuroscience, one key problem is how to identify and hierarchically cluster latent brain functional areas and discover information flow from the thousands of voxels measured in fMRI recordings. Recent advances introduce methods for recovering hidden causal variables in a principled manner [18]. Besides, since causal discovery is a special case of Independent Component Analysis (ICA), recent breakthroughs in identifiable nonlinear ICA without auxiliary variables also shed light on the recovery of the hidden causal structures with general nonlinear causal relations [19].

Applications in Science

In this section, we present several quick examples of the application of causality in science. Since we focus more on computational methods instead of experimental interventions. we just include causal discovery methods on observational data.

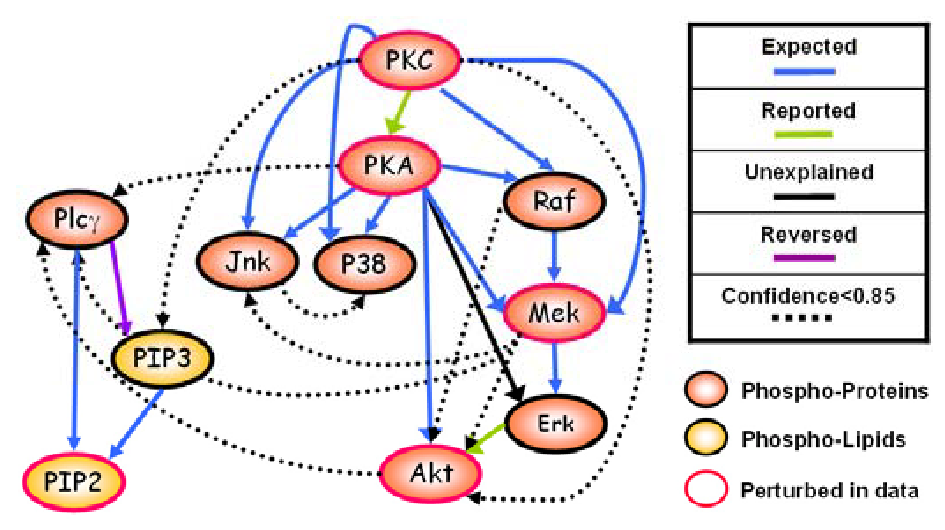
Figure 3: Causal protein-signaling networks (Sachs) [20].

One of the most significant applications of causal discovery in science is in the field of genetics. For example, researchers can use causal discovery techniques to identify genes that play a role in the development of complex diseases such as cancer, heart disease, and mental illness. By understanding the causal relationships between genes and disease, researchers can prioritize potential therapies and predict their efficacy, leading to faster and more effective drug development.

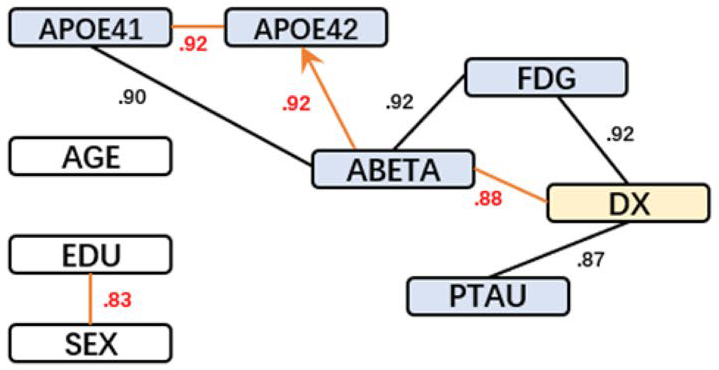
Figure 4: Discovered causal structure among demographic variables, biomarkers, and genetics on data from Alzheimer’s Disease Neuroimaging Initiative (ADNI) database [21].

Another example of causal discovery in science is in the field of pharmacology. Researchers can use it to study the relationships between drugs and their side effects. By understanding these causal relationships, they can predict the likelihood of side effects and design safer and more effective drugs.

In the field of physics, causal discovery can be used to study complex systems such as climate change. For example, scientists can use it to identify the causal relationships between greenhouse gas emissions, deforestation, and global temperatures. This information can be used to make predictions about future climate patterns and inform policy decisions aimed at mitigating the effects of climate change.

In the social sciences, causal discovery has applications in fields such as psychology, sociology, and economics. For example, researchers can use causal discovery techniques to study the relationships between variables such as personality traits, social norms, and economic variables. By understanding these causal relationships, they can gain insights into human behavior and design more effective policies and interventions.

In conclusion, the applications of causal discovery in science are wide-ranging and have the potential to revolutionize our understanding of complex systems and processes. By uncovering the causal relationships between variables, researchers can gain a deeper understanding of the factors that drive these systems and design more effective tools and technologies. The common pipeline for applying causal discovery in real-world problems [1] could be summarized as follows:

Check the data distribution to have a basic understanding of the distribution type and functional relations.
Check whether the preprocessing has distorted the distributions or not. For example, high pass filtering in fMRI software may eliminate the non-Gaussianity in variables.
Check if missing values, selection bias, latent confounders, or other challenges should be considered in the application. If so, specific algorithms could be adopted. Here is a non-exhaustive list of method choices for reference. The implementations of these can be found in causal-learn
- Causal discovery from nonstationary and/or heterogeneous data [22].
- Causal discovery for specific functional model [12, 8, 9].
- Causal discovery with confounders (latent variables) and selection bias [23, 18].
- Causal discovery with missing values [24].
- Causal discovery with discrete or mixed-type data [6].
- Causal discovery with (almost) nonparametric model [25, 6].
Based on the observed distribution type and functional relations between variables, choose the appropriate causal discovery/causal representation learning method.
Make use of the known causal relations, such as those from experiments or domain experts. These relations can serve as the ground truth to test the reasonableness of the result. Besides, one can also use this background knowledge as a constraint to both speed up the algorithm and improve the quality.
If possible, try to find the best practice by testing on the synthetic data first.

Besides learning on observational data, causal inference based on experimental data is also a powerful tool used in scientific research to determine the causal relationships between variables in a system. In experimental settings, researchers deliberately manipulate one or more variables and observe the resulting changes in other variables, allowing them to make causal inferences about the relationship between the manipulated variable and the other variables in the system. This approach is widely used in many fields of science, from biology to social sciences, to establish cause-and-effect relationships between variables. For example, in medicine, clinical trials involve randomly assigning participants to different treatments and observing the resulting changes in health outcomes, allowing researchers to make inferences about the causal effects of the treatments. In social sciences, randomized control trials are used to test the effectiveness of interventions aimed at improving various outcomes, such as education or employment.

At the same time, when manipulation of variables is not possible, counterfactual reasoning allows researchers to compare outcomes from different hypothetical scenarios and infer the causal effects of a variable on another variable. One example of counterfactual reasoning in science is in epidemiology, where researchers may investigate the impact of exposure to a certain risk factor (such as smoking) on a health outcome (such as lung cancer) by comparing the outcomes of individuals who were exposed to the risk factor to those who were not exposed (a counterfactual scenario). In physics, counterfactual reasoning has been used to explore the nature of quantum mechanics by considering the outcomes of experiments that were not actually performed. Counterfactual reasoning is also used in social sciences, such as in policy evaluation, where researchers may use counterfactuals to estimate the impact of an intervention or policy by comparing the outcomes of a group that received the intervention to those of a group that did not.

Tool for causal discovery: causal-learn

Causal-learn is a causal discovery platform led by Prof. Kun Zhang at Carnegie Mellon University (CMU) and developed by multiple teams. Causal-learn is implemented in Python and is based on CMU’s Tetrad causal discovery platform developed in Java, but with additional algorithms and features. It includes classic algorithms and APIs for causal discovery and modular code for researchers to implement their own algorithms. All modules in causal-learn are implemented in Python, avoiding the dependence on R/Java of traditional causal discovery libraries and providing convenience for Python developers. Causal-learn supports:

Constrained-based causal discovery methods;
Score-based causal discovery methods;
Causal discovery methods based on constrained functional causal models;
Hidden causal representation learning;
Permutation-based causal discovery methods;
Granger causal analysis;
Multiple independent basic modules, such as independence tests, scoring functions, graph operations, and evaluation metrics;
More recent causal discovery algorithms such as gradient-based methods.

Besides classical algorithms (e.g., PC and GES) with state-of-the-art implementation, below is a non-exclusive list of how specific types of problems or practical challenges can be addressed by methods in causal-learn. Detailed instruction and usage examples can be found at the documentation of causal-learn.

Causal discovery from nonstationary and/or heterogeneous data: CD-NOD [22].
Causal discovery for specific functional model: post-nonlinear models (PNL) [12], linear, non-Gaussian acyclic models (LiNGAM) [8], and additive noise models (ANM) [9].
Causal discovery with confounders (latent variables) and selection bias: fast causal inference (FCI) [23] and Generalized Independence Noise condition-based method (GIN) [18].
Causal discovery with missing values: missing-value PC (MVPC) [24].
Causal discovery with discrete or mixed-type data: Generalized Score [6].
Causal discovery with (almost) nonparametric model: kernel-based conditional independence test (KCI) [25] and Generalized Score [6].

Causal-learn is designed to modularize the code as much as possible to simplify the development difficulty for researchers. At the same time, by providing concise and efficient code interfaces, users from different fields can easily apply causal discovery algorithms. The whole platform is based on Python, and users no longer need to rely on Java or R environments to fully enjoy the convenience of Python development and use. At the same time, causal-learn provides a simple installation method, and one line of code can deploy the most classic and comprehensive causal recommendation algorithms in the user’s project.

Besides, causal-learn includes official implementations of many classic algorithms and their extensions, such as PC, PNL, LiNGAM, etc. The main authors of these “milestone” algorithms in the field of causal discovery are in the leadership team of causal-learn to guide the direction of platform construction. Therefore, causal-learn provides the most “official” algorithm implementation. By familiarizing with the related codes, users can quickly master the classic algorithms of causal discovery, so as to grasp the overall development of the field and provide inspiration for relevant research.

Moreover, causal-learn has a stable development and maintenance team, and the research team behind it continues to output the latest work in the field of causal discovery. Therefore, users can keep abreast of the latest developments in the field by following the causal-learn algorithm platform, and applying the latest work to different scientific research and production projects in a timely manner.

A quick example

Here we show a quick example of how to use causal-learn to perform causal discovery on observational data. The following example is the PC algorithm:

from causallearn.search.ConstraintBased.PC import pc

cg = pc(data)

# visualization using pydot

cg.draw_pydot_graph()

# or save the graph

from causallearn.utils.GraphUtils import GraphUtils

pyd = GraphUtils.to_pydot(cg.G)
pyd.write_png('simple_test.png')

# visualization using networkx

# cg.to_nx_graph()

# cg.draw_nx_graph(skel=False)

Then we can obtain the causal graph corresponding to the causal process hidden underlying the observational data. More examples can be found in the documentation.

Benchmarks

Here we show a list of benchmark datasets for real-world problems and tasks that might be of interest to readers:

Infant Health and Development Program (IHDP) data: https://www.tandfonline.com/doi/suppl/10.1198/jcgs.2010.08162?scroll=top
Churn for bank customers dataset:https://www.kaggle.com/mathchi/churn-for-bank-customers/
Teleco customer churn https://www.kaggle.com/blastchar/telco-customer-churn
Abalone data: https://archive.ics.uci.edu/ml/datasets/abalone
Boston housing data: https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
Sachs data: https://www.bnlearn.com/research/sachs05/index.html

Learning Resources

Of course, this chapter is just a glance at learning causation for science. If needed, readers are encouraged to explore other learning resources, e.g.,

Books:
- Causation, Prediction, and Search [2].
- The Book of Why: the New Science of Cause and Effect [26].
- The Mind’s Arrows [27].
- Elements of Causal Inference: Foundations and Learning Algorithms [28].
- Causal Inference in Statistics: A Primer [29].
- Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction [30].
Online seminars:

References

[1] Clark Glymour, Kun Zhang, and Peter Spirtes. Review of causal discovery methods based on graphical models. Frontiers in genetics, 10:524, 2019.

[2] Peter Spirtes, Clark N Glymour, Richard Scheines, and David Heckerman. Causation, prediction, and search. MIT press, 2000.

[3] David Maxwell Chickering. Optimal structure identification with greedy search. Journal of machine learning research, 3(Nov):507–554, 2002.

[4] David Heckerman, Dan Geiger, and David M Chickering. Learning bayesian networks: The combination of knowledge and statistical data. Machine learning, 20:197–243, 1995.

[5] Gideon Schwarz. Estimating the dimension of a model. The annals of statistics, pages 461–464, 1978.

[6] Biwei Huang, Kun Zhang, Yizhu Lin, Bernhard Schölkopf, and Clark Glymour. Generalized score functions for causal discovery. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, pages 1551–1560, 2018.

[7] Ignavier Ng, Yujia Zheng, Jiji Zhang, and Kun Zhang. Reliable causal discovery with improved exact search and weaker assumptions. Advances in Neural Information Processing Systems, 34:20308–20320, 2021.

[8] Shohei Shimizu, Patrik O Hoyer, Aapo Hyvärinen, Antti Kerminen, and Michael Jordan. A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(10), 2006.

[9] Patrik O Hoyer, Dominik Janzing, Joris M Mooij, Jonas Peters, Bernhard Schölkopf, et al. Nonlinear causal discovery with additive noise models. In NIPS, volume 21, pages 689–696. Citeseer, 2008.

[10] Kun Zhang and Aapo Hyvärinen. Causality discovery with additive disturbances: An information-theoretical perspective. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2009, Bled, Slovenia, September 7-11, 2009, Proceedings, Part II 20, pages 570–585. Springer, 2009.

[11] Kun Zhang and Lai-Wan Chan. Extensions of ica for causality discovery in the hong kong stock market. In Neural Information Processing: 13th International Conference, ICONIP 2006, Hong Kong, China, October 3-6, 2006. Proceedings, Part III 13, pages 400–409. Springer, 2006.

[12] K Zhang and A Hyvärinen. On the identifiability of the post-nonlinear causal model. In 25th Conference on Uncertainty in Artificial Intelligence (UAI 2009), pages 647–655. AUAI Press, 2009.

[13] Kun Zhang, Zhikun Wang, Jiji Zhang, and Bernhard Schölkopf. On estimation of functional causal models: general results and application to the post-nonlinear causal model. ACM Transactions on Intelligent Systems and Technology (TIST), 7(2):1–22, 2015.

[14] Gustavo Lacerda, Peter L Spirtes, Joseph Ramsey, and Patrik O Hoyer. Discovering cyclic causal models by independent components analysis. arXiv preprint arXiv:1206.3273, 2012.

[15] Patrik O Hoyer, Shohei Shimizu, Antti J Kerminen, and Markus Palviainen. Estimation of causal effects using linear non-Gaussian causal models with hidden variables. International Journal of Approximate Reasoning, 49(2):362–378, 2008.

[16] Biwei Huang, Kun Zhang, Pengtao Xie, Mingming Gong, Eric P Xing, and Clark Glymour. Specific and shared causal relation modeling and mechanism-based clustering. Advances in Neural Information Processing Systems, 32, 2019.

[17] Kun Zhang, Jiji Zhang, Biwei Huang, Bernhard Schölkopf, and Clark Glymour. On the identifiability and estimation of functional causal models in the presence of outcome-dependent selection. In UAI, 2016.

[18] Feng Xie, Ruichu Cai, Biwei Huang, Clark Glymour, Zhifeng Hao, and Kun Zhang. Generalized independent noise condition for estimating latent variable causal graphs. In NeurIPS, 2020.

[19] Yujia Zheng, Ignavier Ng, and Kun Zhang. On the identifiability of nonlinear ICA: Sparsity and beyond. In Advances in Neural Information Processing Systems, 2022.

[20] Karen Sachs, Omar Perez, Dana Pe’er, Douglas A Lauffenburger, and Garry P Nolan. Causal protein-signaling networks derived from multiparameter single-cell data. Science, 308(5721):523–529, 2005.

[21] Xinpeng Shen, Sisi Ma, Prashanthi Vemuri, and Gyorgy Simon. Challenges and opportunities with causal discovery algorithms: application to alzheimer’s pathophysiology. Scientific reports, 10(1):2975, 2020.

[22] Biwei Huang, Kun Zhang, Jiji Zhang, Joseph D Ramsey, Ruben Sanchez-Romero, Clark Glymour, and Bernhard Schölkopf. Causal discovery from heterogeneous/nonstationary data. J. Mach. Learn. Res., 21(89):1–53, 2020.

[23] Peter L Spirtes, Christopher Meek, and Thomas S Richardson. Causal inference in the presence of latent variables and selection bias. Uncertainty in Artificial Intelligence, 1995.

[24] Ruibo Tu, Cheng Zhang, Paul Ackermann, Karthika Mohan, Hedvig Kjellström, and Kun Zhang. Causal discovery in the presence of missing data. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 1762–1770. PMLR, 2019.

[25] Kun Zhang, Jonas Peters, Dominik Janzing, and Bernhard Schölkopf. Kernel-based conditional independence test and application in causal discovery. arXiv preprint arXiv:1202.3775, 2012.

[26] Judea Pearl and Dana Mackenzie. The book of why: the new science of cause and effect. Basic books, 2018.

[27] Clark N Glymour. The mind’s arrows: Bayes nets and graphical causal models in psychology. MIT press, 2001.

[28] Jonas Peters, Dominik Janzing, and Bernhard Schölkopf. Elements of causal inference: foundations and learning algorithms. The MIT Press, 2017.

[29] Judea Pearl, Madelyn Glymour, and Nicholas P Jewell. Causal Inference in Statistics: A Primer. John Wiley & Sons, 2016.

[30] Guido W Imbens and Donald B Rubin. Causal inference in statistics, social, and biomedical sciences. Cambridge University Press, 2015.