Manifesto
Ever since the time of Isaac Newton, there have been two different paradigms for scientific research: the Keplerian paradigm and the Newtonian paradigm.


The Keplerian paradigm, often referred to as the “data-driven” approach, expects to extract new physical rules or trends through data analysis and utilize these rules to solve actual problems. The discovery of Kepler’s laws of planetary motion was the canonical implementation of this paradigm. Nowadays, many successful examplesbioinformatics and cheminformatics have demonstrated the effectiveness of this paradigm in areas from multi-scale modeling, protein structure prediction, to drug discoveryincluding drug discovery or disease treatment.
The Newtonian paradigm is based on working from first principles, with the aim to figure out fundamental physical rules that govern the world as we know it. Based on these principles, scientists are able to explain most of the experimentally observed phenomenons. One of the most successful theories is quantum mechanics because it almost prepares us with all necessary laws for much of engineering and natural sciences. However, as pointed out by Dirac, “the exact application of these laws leads to equations much too complicated to be solved”. The central difficulty is called “the curse of dimensionality”, i.e., the problems we are encountered are actually too high-dimensional and cannot be solved efficiently. For a long time, natural scientists have only had limited ability to handle these equations with at most thousands of variables.
Machine learning, especially deep learning (or generally AI) techniques emerge as effective tools to approximate arbitrary high-dimensional functions as illustrated by its unprecedented success in computer vision (CV) and natural language processing (NLP). In the Newtonian paradigm, AI methods have been applied to incorporate physical laws to solve more much complicated problems or system simulations than toy examples. In the Keplerian paradigm, AI can be directly applied to analyze and learn from data in an end-to-end manner. With the promises of AI in solving real and challenging scientific problems, “AI for Science” (AI4Science) has become established as a new term and prevailed in both AI and scientific research communities. In the past few years, successful applications of AI methods have opened up a wide research avenue for both communities, from AlphaFold2 [1] that solves the 50-year-old protein structure prediction puzzle, DeePMD [2] that extending ab initio simulation to unprecedentedly large scales, to controlling nuclear reactor with AI agents [3]. The new paradigm of scientific research empowered by AI has been formed, and aforementioned successful examples have paved the way for this new paradigm. However, as scientific discovery has a very broad scope with many different disciplines many grand challenges that are critical to our lives still remain unsolved. Despite the early success, we have to acknowledge that AI for Science is still nascent and requires joint efforts from both AI and scientific communities.
We are living in an era with the opportunity and means to tackle grand challenges in scientific discovery. To facilitate this emergent field and bridge gaps between AI and scientific communities, this blog aims to equip researchers in the AI community with some basic scientific knowledge and an overview of new challenges in scientific discovery, which may appear significantly different from common AI application areas such as computer vision and speech recognition.
Success of AI in Scientific Discovery
Protein Structure Prediction
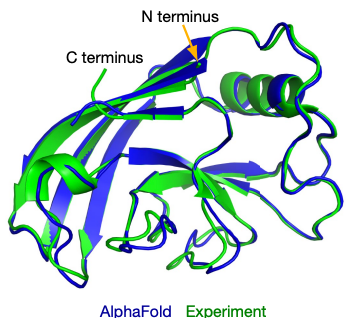
When it comes to AI for Science, arguably the most famous and successful example of AI-advanced scientific discovery is AlphaFold2 which addresses the problem of accurately predicting protein 3D structures from their sequence, one of the “holy grail” problems in structural biology. The structures of proteins are essential to their biological functions and accurate 3D modeling at the atomistic level is significant for a variety of field from drug discovery to synthetic biology. However, resolving structures experimentally is highly expensive and time-consuming, so computational methods to predict accurate protein structures have long been studied, represented by the series of CASP competitions [4]. Anfinsen’s hypothesis, stating that for most proteins, the native structures in standard physiological environments are determined solely by the proteins’ amino acid sequences, grounds the study of computational method for the protein structure prediction problem. Traditionally, structural biologists utilize “homology modeling” to make such predictions. In those methods, multiple proteins, whose sequences are similar to the query one and structures have already been resolved experimentally, will be found. These structures will be then be assembled to provide the predicted result. The accuracy of homology modeling depends heavily on sequence identity, and sometimes fails to reach a satisfying level. Deep learning methods, however, have stronger ability to discover correlations between sequences and structures. With carefully-designed attention-based neural networks and multiple-sequence-alignment (MSA) information, in 2020, the AlphaFold2 model achieved an astonishing average RMSD of 0.96 angstroms on the test cases in the prestigious CASP competition. Such accuracy is even comparable to experimental errors and AF2 was considered to make a breakthrough in solving this 50-year structural biological puzzle.
Multi-scale Modeling
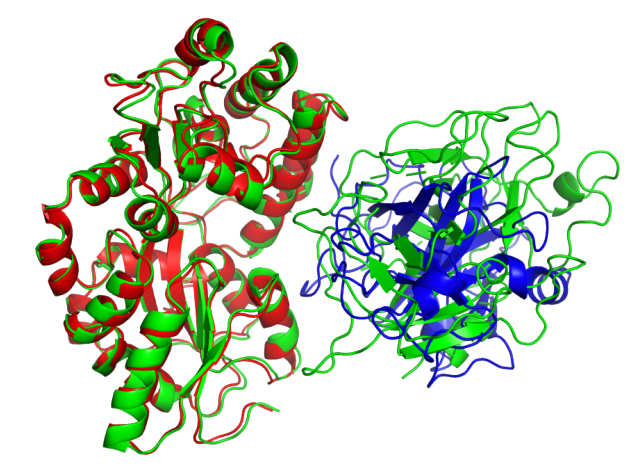
As mentioned in the manifesto, the principles of our physical world are almost completely known but the mathematical equations are too complicated to be solved accurately. Therefore, for problems at different time and space scales, scientists have to develop different computational methods with the necessary approximations to reduce the computational complexity which is called multi-scale modeling in computational science. In this area, ab initio and classical molecular dynamics (shortened as AIMD and classical MD) are two widely used techniques. However, there has been a longstanding trade-off problem between the accuracy and efficiency of these methods. Specifically, in AIMD, the energy and forces of given systems are calculated by quantum mechanics (usually density functional theory or DFT), thus it is more accurate but more time-consuming. The computational complexity is $O\left (N^3\right)$, where $N$ is the number of electrons in the systems. In classical MD, the potential energy surface is given by fixed mathematical forms with manually curated parameters (named “force fields”), so it is much faster ($ O\left(N\right)$) but less accurate. Recently, AI methods have been largely developed to bridge this gap [5,6,7]. Specifically, researchers designed neural networks that preserving necessary physical symmetries and generated a neural representation of atomic configurations which could be used to fit DFT-level potential energy surfaces. However, it still requires large-scale dataset to train such models. Concurrent learning [8] workflows are here to rescue, by heuristically exploring the configuration space to collect as few data as possible. In this manner, construction of neural network potentials becomes more automatic, which further enables a variety of applications in complex systems in condensed matters as well as material science [9].
Why is AI for Science different?
Data is Important
Undoubtedly, AI methods rely on datasets with both high-quality and high-quantity to achieve excellent performance in solving problems, which has been demonstrated by ImageNet [10] , Cifar-10 [11], etc. This is also very true for scientific problems, examplified by RCSB Protein Data Bank (PDB) [12]. This database, containing approximate 200,000 data entries and maintained by researchers all over the world for over 40 years, is one of the best database for experimentally resolved biomolecular structures. Deep learning methods would never reach such a success without efforts from maintainers of PDB. In particular, scientific problems usually involve real and challenging scenarios for many AI-interested topics, e.g., out-of-distribution generalization, low-data regime learning, etc. And it is often the case that in many topics, no high-quality dataset is available to generate effective deep learning models. Therefore, it is encouraged that AI researchers to pay more attention to data collection and structuralization, during which domain expertise and joint efforts are required. % Some examples include learning from structures studied in several years ago to predict structures of researchers’ interest today for out-of-distribution generalization, learning from highly expensive quantum property data to predict property for new data (low-data regime), etc.
Problem Formulation
Many scientific discovery problems are much more complex than simple classification or regression tasks. For AI researchers, scientific problems have to be decomposed and well-formulated to an extent that inputs, outputs, and objective functions (often needs to be differentiable) can be clearly defined. For example, “drug design” is a huge pipeline which consists of a sequence of steps and is obviously not a well-formulated problem itself. Instead, we can decompose this problem into different pieces that are AI-solvable: molecular property prediction for virtual screening molecular databases, molecular generation for proposing better drug candidates, etc. Problems failed to be compliant with this standard are often referred to as “dirty” ones, and are unlikely to be addressed solely with AI methods.
Real-world Challenges in AI for Science
Next Steps in Protein Structure Prediction
Represented by AlphaFold2 [1], a variety of AI-based protein structure prediction models [13,14] successfully solve the protein structure prediction problem, but it is only the first step towards understanding protein structures and functions. There are still many remaining challenges to be solved:
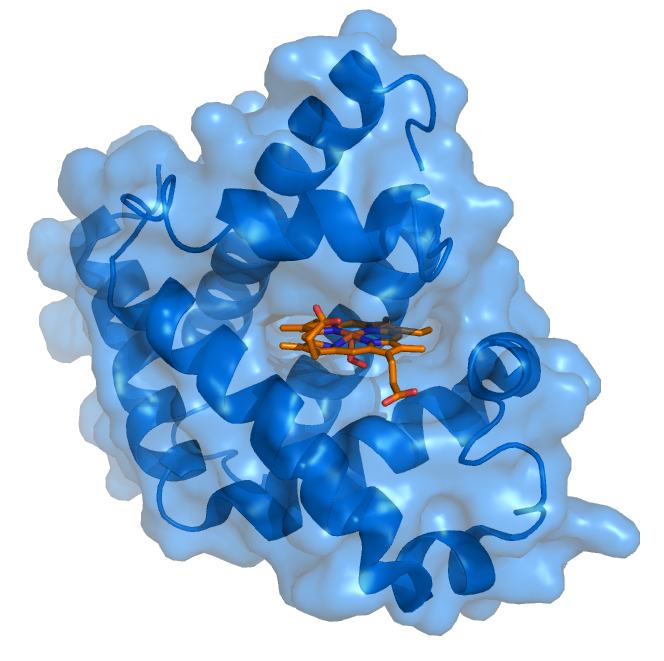
Protein Multimers Current predictive models of protein structure can only provide reliable results for monomers (single peptide chain). But in reality, peptide chains can interact with each other and form complexes (multimers). In many scenarios, only by doing so can the proteins perform their biological functions correctly. In structural biology, such behavior is defined as quarternary protein structure.
Protein-ligand Complex Protein-ligand interactions and the induced-fit models are key to understanding drugs’ potency. Small organic molecules often interact with a certain area (referred to as a pocket) in target proteins and may cause the protein structure to change significantly. Traditional computational methods, such as molecular docking, model the protein-ligand binding free energies with physical-based scoring functions, which are parametrized in an empirical and error-prune way. AI models will be a breakthrough in this area if accurate prediction of the ligand binding pose, and/or the protein structural changes during the ligand binding process can be made.
Protein Conformation Ensembles Most of the recent successful models are based on multiple sequence alignment (MSA), which can be viewed as an augmented version of “homologous modeling”. The scientific logic behind this is that proteins follow rules of evolution, so more or less, any protein found naturally is subject to have some structural similarities with those proteins in other organisms which some have been studied before. However, there are still a variety of proteins that are de novo-designed (manually designed) or lacking MSA, current models fail to provide reliable prediction results. Thus one promising direction of AI-based protein structure prediction may be the development of MSA-free models.
Quantum Mechanics
One of the central goals in quantum mechanics is to find accurate solutions (wave functions and energies) to Schrödinger equations on real systems, which is hindered by many-body problems because the dimensionality of the equation is $3N$, where $N$ is the number of electrons (and a real system can easily have hundreds of electrons, where the many-body Schrödinger equations can not be solved exactly. To compromise, researchers have come up with many approximation methods, such as DFT (density functional theory), to make the computational cost acceptable by sacrificing some accuracy. This work have reached great achievements in many areas such as material science, but in cases where the DFT results are not accurate enough, researchers have to rely on more accurate but more time-consuming methods (CCSD(T), with a computation complexity of $O\left(N^7\right)$). Recent work, such as DeePKS [15] and DM21 [16] have been proposed to tackle this issue with AI models, but are still far from perfect. One particular challenge is how to represent an anti-symmetric function under permutation in a neural-network manner (wave functions of electrons are of this property).
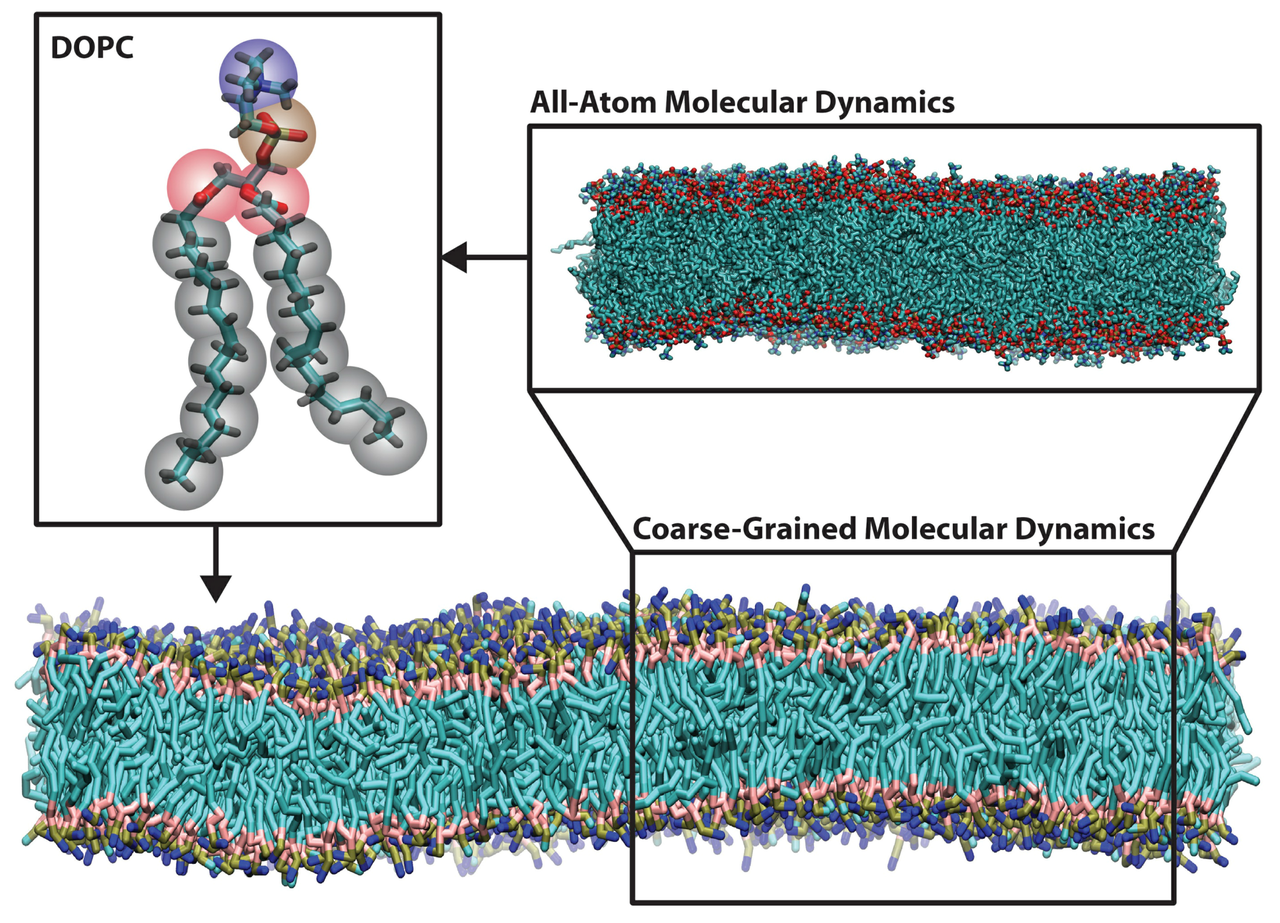
Molecular Dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, providing a view of the dynamic “evolution” of the system. The trajectory can be considered as a sample under the Boltzmann distribution of a given system and temperature. Thus, many thermodynamic properties such as density and free energy can be calculated by MD.
General neural-network-based force field Although deep learning methods have already shown their capabilities in accelerating AIMD, a neural network potential able to be generalized to different systems and simulation settings is of high practical value. This could be achieved by pre-training treatment and thus repeated work can be avoided, as users will no longer need to establish a model from scratch, but fine-tune the pre-trained models against specific systems instead. For example, a model describing arbitrary organic molecules at a very accurate quantum mechanics level will be useful in drug design, and a model describing any components of alloy/materials is valued in material science. Besides, the requirement of higher transferability also challenge current methods with more generalizable representation of atomic configuration, which further brings demand to architecture enhancement.
Coarse-grained models Simulation of extremely large and complicated systems, such as a whole virus, needs coarse-grained force fields that treat several atoms as one “bead”. Then the interactions between these beads are expected to reflect certain properties of interest, such as free energy or conformation distribution. However, it is nontrivial to find optimal forms and parameters to describe such interactions, and currently there are no general protocols like empirical atomistic force fields. AI models may be an effective tool just as they are between DFT/AIMD and classical MD, but more research need to be conducted to answer questions including what targets to fit, how to generate training data efficiently.
Enhanced sampling Enhanced sampling assists to overcome free energies barriers in a molecular dynamic simulation. If the free energy landscape of a given system is not smooth, the simulation will be stuck in one local minimal and ergodicity in molecular dynamics simulation will not be satisfied. This phenomenon is manifested by inadequate sampling over the whole landscape, especially over transition states or other local minima, and occurs frequently in simulation of biological systems. Computational chemists have employed bias-potential-based techniques (such as meta-dynamics [17], and umbrella sampling [18]) to enhance sample efficiency. But these methods require well-defined collective variables (CVs) and fail to handle situations where the number of CVs is large. The key challenge is how to learn an accurate representation of the free energy surface (FES) with high-dimensional CVs. AI models have recently been introduced, e.g., NN-VES [18], Reinforced Dynamics [19], and NN-based CV selections [20,21]. The main challenges lie in better models with generalizability and more effective workflows to take training data generation into consideration [22].
Partial differential equations
High dimensional partial differential equations (PDEs) arise in many scientific problems. Notable examples include high dimensional nonlinear Black-Scholes equations in finance, many electronic Schrödinger equations in quantum mechanics, and high dimensional Hamilton-Jacobi-Bellman equations in control theory. However, traditional numerical algorithms like finite difference or finite element methods suffer from the curse of dimensionality and are unable to deal with PDEs beyond 10 dimensions. The practical success of deep-learning-based PDE solvers such as physics-informed neural networks and deep BSDE method shows the ability of the deep neural networks to efficiently approximate the solutions of high dimensional PDEs. Hence, once we can reformulate the PDE by a variational problem, deep learning techniques can be easily applied to the variational problem and the original PDE can be solved. Successful examples in this direction include the deep Ritz method[23] the deep BSDE method[1] , and Physics-informed neural networks[24]
-
Variational problem: Find the maxima or minima of a functional, which maps functions to scalars, over a given domain.
-
Finite difference method: A class of numerical algorithms to solve the differential equations. It approximates the derivative or partial derivative by finite differences and solves the resulting linear or nonlinear systems.
-
Finite element method: A class of numerical algorithms to solve the differential equations. It converts the differential equations to a variational problem, uses a finite-dimensional linear space to approximate the domain of the variational problem, and solves the variational problem over the finite-dimensional linear space.
Control theory
Control algorithms are widely used in engineering and industry, which aim to govern the application of system inputs to drive the dynamic system to satisfying specific conditions. Since the time of Bellman [25] , a long-lasting problem in control theory is to solve the high dimensional closed-loop control problems, which aims to find the policy function: the input as a function of the state. Indeed, the terminology “curse of dimensionality” was originally coined by Bellman in order to highlight these difficulties. The practical success of deep learning shows that deep neural networks can approximate high dimensional functions and hence raise the hope to solve high dimensional closed-loop control problems. Although this field is still immature and faces many challenges such as stability and robustness of policy function, pioneering works [24,26] show the potential of this field. Another related field is reinforcement learning. Roughly speaking, control algorithms and reinforcement learning problems solve the same problems. However, in contrast, to control algorithms, which make heavy use of the underlying models, reinforcement learning algorithms make minimum use of the model. Comparison and combination of control algorithms and reinforcement learning algorithms are interesting topics and helpful if one wants to deal with complex practical problems.
- Reinforcement learning: Reinforcement learning concerns how an agent takes actions to maximize the long-term reward when faced with an unknown environment. One feature of the reinforcement learning algorithm is that it does not require the exact form of the underlying model.
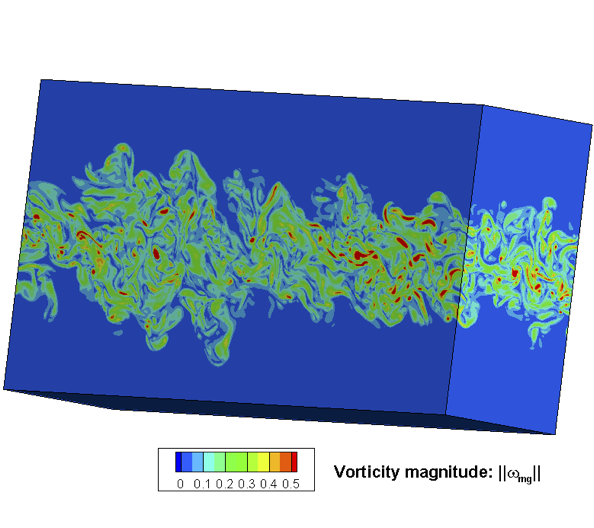
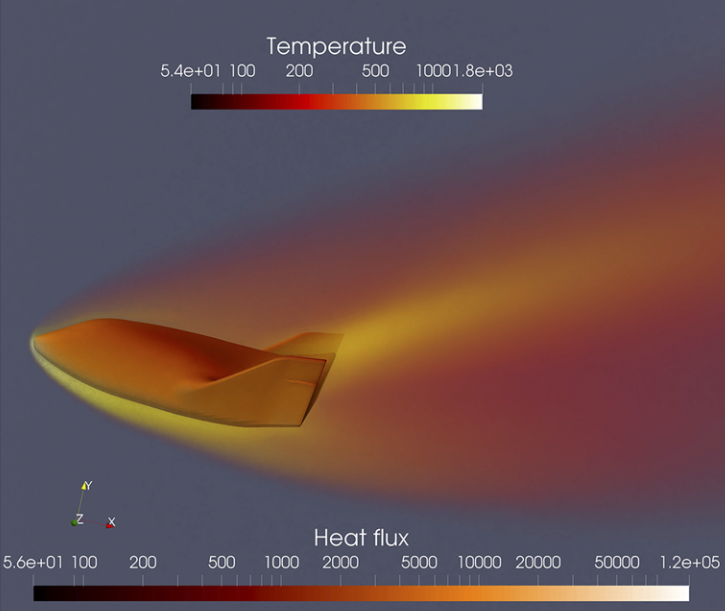
Fluid Mechanics
Fluid mechanics studies the systems with fluid (liquids, gases, and plasmas) at rest and in motion [27,28,29]. Many scientific and engineering disciplines get involved with fluid mechanics (as shown in Figure above), including astrophysics, oceanography, meteorology, aerospace engineering, chip industry, and physics-based animation. Overall, the fluid mechanics can be roughly divided into inviscid flows vs. viscous flows, laminar flows vs. turbulence, incompressible flows vs. compressible flows, continuum flows vs. rarefied flows, single-phase flows vs. multiphase flows, Newtonian flows vs. non-Newtonian flows, etc.
Mathematical analysis, experimental studies, and numerical simulations are three major approaches to exploring fluid mechanics. Fundamentally, a fluid system is assumed to be governed by mathematical equations in the conservation of mass, momentum, and energy. In different physical modeling scales, the governing equations of fluid are in different forms [30], the newton dynamics, Boltzmann equation, Euler or Navier-Stokes equations (NSE), and coarse-grained turbulence models. In the hierarchy of governing equations, the hyperbolic Euler equations for inviscid flows are usually utilized to validate the performance of the numerical scheme of its accuracy, efficiency, and robustness. Additionally, the NSE is widely used in continuum viscous fluid mechanics, while the Boltzmann equation works well in rarefied gas dynamics. With the rapid growth of high-performance computing, numerical simulation called computational fluid dynamics (CFD) not only gradually becomes the indispensable tool to validate the key mathematical conclusions and experimental observations in fluid dynamics, but also provides more abundant and practical fluid information (macroscopic velocities, pressure and temperature distribution, drag and lift force, heat load, noise level) for engineering applications. With the aid of AI methods, research on numerical and experimental fluid mechanics may be improved.
- Design data-driven turbulence models, such as modeling high-Reynolds number wall-bounded turbulent flows and complex separated turbulent flows [31] (i.e., the simulation and design in advanced aircraft).
- Conduct data assimilation in flow fields, which combines the sparse measured data and numerical solutions together to provide more complete and accurate flow fields (i.e., the prediction of ocean circulation, weather forecast, and city environment simulations).
- Refresh multiphase and multiscale fluid models, which modify the ad-hoc models of turbulence combustion, multiphase flows, and rarefied gas dynamics (i.e., efficient moment closure models for simulating rarefied flows).
See the opportunities - Why AI for Science?
- Challenging scenarios. For AI algorithms, scientific applications are usually much more challenging, compared to common applications in images, texts, or audio, where “rules” are defined by humans. Science is about finding and understanding the nature, so it is usually more challenging.
- Real-world impacts. Scientific discovery works for the good of human beings. For example, boosting drug design will reduce the price of drugs and save more people’s lives.
- New discovery. Curiosity is the nature of human beings that motivates the development of science. As Kepler derived the laws of planetary motions hundreds of years ago, we are in an era in which AI may help us to discover new science systematically.
Mind your steps
- Be careful with data. Datasets in scientific problems have many problems: it may be highly-screwed, with 99\% positive cases and only 1\% negative cases, because researchers will not publish their bad results; it may be very small, because much data is hard to generate and collect; it may be very dirty, for example, some experimental results are noisy and not reliable.
- Understand the problems. Scientific concepts are not as easy to understand as classifying cats and dogs in computer vision. Take a humble and respectful manner toward scientific problems and learn more scientific backgrounds (physics, chemistry, biology, etc.) about the problem of interest. Understand the reason for solving the problem and the practical application of the research are the key to success.
- Be patient. “Rome was not built in a day.” Scientific problems are often challenging and taking years to solve. But don’t be afraid if you miss any of the deadlines for NeurIPS/ICML/ICLR, good work will be recognized and published and become impactful eventually.
- Enjoy interdisciplinary collaborations. Good collaborations between AI and Science communities are key to make impactful work both in terms of real-world challenges and methodologies. Be open-minded while talking to people from the other community.
A Roadmap of Basic Scientific Knowledge
Classical Mechanics
- Kibble, Tom, and Frank H. Berkshire. Classical mechanics. world scientific publishing company, 2004.Classical Mechanics
Statistic Mechanics:
- Tuckerman, Mark. Statistical mMechanics: tTheory and mMolecular sSimulation. Oxford university press, 2010. Mark E. Tuckerman
- Pathria, Raj Kumar.Statistical Statistical mMechanics. Elsevier (R. K. Pathria, Paul D. Beale, 2016.1)
Quantum Mechanics:
- A. Szabo, A., and N. S. Ostlund. “, Modern Quantum Chemistry (Dover.” New York (, 1996).
- L. Piela, Lucjan. Ideas of qQuantum cChemistry, 2nd Ed. (Elsevier, 2006.14)
- Sholl, David S., and Janice A. Steckel. Density functional theory: aA practical introduction. John Wiley & Sons (David Sholl, Janice A Steckel, 2011.09)
Solid State Physics:
- Kittel, Charles. “Introduction to Solid State Physics Solution Manual.” (2021). (Charles Kittel, 2004)
Multi-scale Modeling:
- Weinan, E. Principles of mMultiscale mModeling. Cambridge University Press (Weinan, E, 2011.)
Control Theory:
- Evans, Lawrence C. “An introduction to mathematical optimal control theory version 0.2.” Lecture notes available at http://math. berkeley. edu/~ evans/control. course. pdf ( (L.C. Evans, 1983).
Partial Differential Equations:
- Evans, Lawrence C. Partial dDifferential eEquations. Vol. 19. American Mathematical Soc. (L. C. Evans, 2010.)
Fluid Dynamics:
- Kundu, Pijush K., Ira M. Cohen, and David R. Dowling. Fluid mechanics. Academic pressFluid mechanics (P. K. Kundu, I. M. Cohen \& D. R. Dowling, 2015.5)
References
[1] John Jumper, Richard Evans, Alexander Pritzel, Tim Green, Michael Figurnov, Olaf Ronneberger, Kathryn Tunyasuvunakool, Russ Bates, Augustin Žídek, Anna Potapenko, Alex Bridgland, Clemens Meyer, Simon A A Kohl, Andrew J Ballard, Andrew Cowie, Bernardino Romera-Paredes, Stanislav Nikolov, Rishub Jain, Jonas Adler, Trevor Back, Stig Petersen, David Reiman, Ellen Clancy, Michal Zielinski, Martin Steinegger, Michalina Pacholska, Tamas Berghammer, Sebastian Bodenstein, David Silver, Oriol Vinyals, Andrew W Senior, Koray Kavukcuoglu, Pushmeet Kohli, and Demis Hassabis. Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873):583–589, August 2021.
[2] Linfeng Zhang, Jiequn Han, Han Wang, Roberto Car, and Weinan. Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett., 120(14), April 2018.
[3] Jonas Degrave, Federico Felici, Jonas Buchli, Michael Neunert, Brendan Tracey, Francesco Carpanese, Timo Ewalds, Roland Hafner, Abbas Abdolmaleki, Diego de las Casas, Craig Donner, Leslie Fritz, Cristian Galperti, Andrea Huber, James Keeling, Maria Tsimpoukelli, Jackie Kay, Antoine Merle, Jean-Marc Moret, Seb Noury, Federico Pesamosca, David Pfau, Olivier Sauter, Cristian Sommariva, Stefano Coda, Basil Duval, Ambrogio Fasoli, Pushmeet Kohli, Koray Kavukcuoglu, Demis Hassabis, and Martin Riedmiller. Magnetic control of tokamak plasmas through deep reinforcement learning. Nature, 602(7897):414–419, February 2022.
[4] CASP competitions 2022. https://predictioncenter.org/
[5] Justin S Smith, Olexandr Isayev, and Adrian E Roitberg. Ani-1: an extensible neural network potential with dft accuracy at force field computational cost. Chemical science, 8(4):3192–3203, 2017.
[6] Linfeng Zhang, Jiequn Han, Han Wang, Wissam Saidi, Roberto Car, and Weinan E. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Advances in Neural Information Processing Systems, 31, 2018.
[7] Oliver T Unke and Markus Meuwly. Physnet: A neural network for predicting energies, forces, dipole moments, and partial charges. Journal of chemical theory and computation, 15(6):3678–3693, 2019.
[8] Yuzhi Zhang, Haidi Wang, Weijie Chen, Jinzhe Zeng, Linfeng Zhang, Han Wang, and Weinan. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun., 253(107206):107206, August 2020.
[9] Tongqi Wen, Linfeng Zhang, Han Wang, E Weinan, and David J Srolovitz. Deep potentials for materials science. Materials Futures, 2022.
[10] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255. Ieee, 2009.
[11] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
[12] Helen M Berman, John Westbrook, Zukang Feng, Gary Gilliland, Talapady N Bhat, Helge Weissig, Ilya N Shindyalov, and Philip E Bourne. The protein data bank. Nucleic acids research, 28(1):235–242, 2000.
[13] Minkyung Baek, Frank DiMaio, Ivan Anishchenko, Justas Dauparas, Sergey Ovchinnikov, Gyu Rie Lee, Jue Wang, Qian Cong, Lisa N Kinch, R Dustin Schaeffer, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science, 373(6557):871–876, 2021. 52
[14] Jian Peng and Jinbo Xu. Raptorx: exploiting structure information for protein alignment by statistical inference. Proteins: Structure, Function, and Bioinformatics, 79(S10):161–171, 2011.
[15] Yixiao Chen, Linfeng Zhang, Han Wang, and Weinan E. Deepks: A comprehensive data-driven approach toward chemically accurate density functional theory. Journal of Chemical Theory and Computation, 17(1):170–181, 2021. PMID: 33296197.
[16] James Kirkpatrick, Brendan McMorrow, David H. P. Turban, Alexander L. Gaunt, James S. Spencer, Alexander G. D. G. Matthews, Annette Obika, Louis Thiry, Meire Fortunato, David Pfau, Lara Román Castellanos, Stig Petersen, Alexander W. R. Nelson, Pushmeet Kohli, Paula Mori-Sánchez, Demis Hassabis, and Aron J. Cohen. Pushing the frontiers of density functionals by solving the fractional electron problem. Science, 374(6573):1385–1389, 2021.
[17] Alessandro Laio and Michele Parrinello. Escaping free-energy minima. Proceedings of the National Academy of Sciences, 99(20):12562–12566, 2002.
[18] Glenn M Torrie and John P Valleau. Nonphysical sampling distributions in monte carlo free-energy estimation: Umbrella sampling. Journal of Computational Physics, 23(2):187–199, 1977.
[19] Luigi Bonati, Yue-Yu Zhang, and Michele Parrinello. Neural networks-based variationally enhanced sampling. Proceedings of the National Academy of Sciences, 116:201907975, 08 2019.
[20] Linfeng Zhang, Han Wang, and Weinan E. Reinforced dynamics for enhanced sampling in large atomic and molecular systems. The Journal of chemical physics, 148(12):124113, 2018.
[21] Dongdong Wang, Yanze Wang, Junhan Chang, Linfeng Zhang, Han Wang, et al. Efficient sampling of high-dimensional free energy landscapes using adaptive reinforced dynamics. Nature Computational Science, 2(1):20–29, 2022.
[22] Luigi Bonati, Valerio Rizzi, and Michele Parrinello. Data-driven collective variables for enhanced sampling. The Journal of Physical Chemistry Letters, 11:2998–3004, 04 2020.
[23] Andrew W Senior, Richard Evans, John Jumper, James Kirkpatrick, Laurent Sifre, Tim Green, Chongli Qin, Augustin Žídek, Alexander W R Nelson, Alex Bridgland, Hugo Penedones, Stig Petersen, Karen Simonyan, Steve Crossan, Pushmeet Kohli, David T Jones, David Silver, Koray Kavukcuoglu, and Demis Hassabis. Improved protein structure prediction using potentials from deep learning. Nature, 577(7792):706–710, January 2020.
[24] Richard Evans, Michael O’Neill, Alexander Pritzel, Natasha Antropova, Andrew Senior, Tim Green, Augustin Žídek, Russ Bates, Sam Blackwell, Jason Yim, Olaf Ronneberger, Sebastian Bodenstein, Michal Zielinski, Alex Bridgland, Anna Potapenko, Andrew Cowie, Kathryn Tunyasuvunakool, Rishub Jain, Ellen Clancy, Pushmeet Kohli, John Jumper, and Demis Hassabis. Protein complex prediction with AlphaFold-Multimer. October 2021.
[25] E Weinan. The dawning of a new era in applied mathematics. Notices of the, volume 68. American Mathematical Society, 2021.
[26] Linfeng Zhang, Jiequn Han, Han Wang, Wissam A Saidi, Roberto Car, and Weinan E. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. May 2018.
[27] Pijush K Kundu, Ira M Cohen, and Howard H Hu. Fluid Mechanics. Academic Press Inc. (London), London, England, 3 edition, December 2004. 53
[28] Frank M White. Viscous fluid flow (int’l ed). McGraw-Hill Professional, New York, NY, 3 edition, April 2005.
[29] David J Acheson. Elementary fluid dynamics. Clarendon Press, 2009.
[30] Kun Xu. Direct modeling for computational fluid dynamics: Construction and application of unified gas-kinetic schemes. Advances In Computational Fluid Dynamics. World Scientific Publishing, Singapore, Singapore, March 2015.
[31] Karthik Duraisamy, Gianluca Iaccarino, and Heng Xiao. Turbulence modeling in the age of data. March 2018.